Every time AI labs release new models, we see an evaluation metric called $\text{pass@}k$, where $k$ can be any integer number such as $\text{pass@}1$. It might sound like passing a test at the $k$th attempt, but this metric is far more sophisticated and plays a crucial role in how we build reliable AI applications in production.

As an example, here’s OpenAI GPT-5’s performance on AIME.

OpenAI GPT-5

$\text{pass@k}$ does not mean the model passing a test in $k$ attempts. It is calculated using an estimator.

Most terms in AI, Machine Learning, and Reinforcement Learning have specific technical definitions that deviate from plain English, from accuracy and agents to recall and retrieval-augmented generation (RAG). Understanding $\text{pass@}k$ is particularly important because it directly influences how we evaluate models and design sampling strategies for compound AI systems.

This blog post aims to demystify what $\text{pass@}k$ means, explain the mathematics behind its calculation, and show you how to leverage this metric to build more reliable AI applications.

Due to the inherent randomness in model outputs, we don’t know the true $\text{pass@}k$ value. Instead, we must estimate it based on a finite number of experiments or samples. The formula we use to calculate $\text{pass@}k$ is called an estimator.

Unbiased Estimator

In statistics, an unbiased estimator is a method for estimating a population parameter like a mean or probability that gives the correct value on average. “Unbiased” means the estimator’s expected value equals the true value it’s trying to estimate across many samples.

For example, if you’re estimating the average height of people in a city $\mu$, an unbiased estimator, e.g., the sample mean, will, over many samples, average out to $\mu$. Mathematically, if $\theta$ is the parameter and $\hat{\theta}$ is the estimator, it’s unbiased if:

\[E(\hat{\theta}) = \theta\]

where $E(\hat{\theta})$ is the expected value of the estimator.

The Biased Estimator Problem

Lets call our emperical estimate of $\text{pass@}k$ as $\hat{p}$. The naive approach to calculate $\hat{p}$ can be done by running n trials and dividing the number of successful trials by n. For example, if 30 out of 100 code samples are correct, then $\hat{p} = 30/100 = 0.3$.

Using this empirical probability, we can try to estimate $\text{pass@}k$ with the formula:

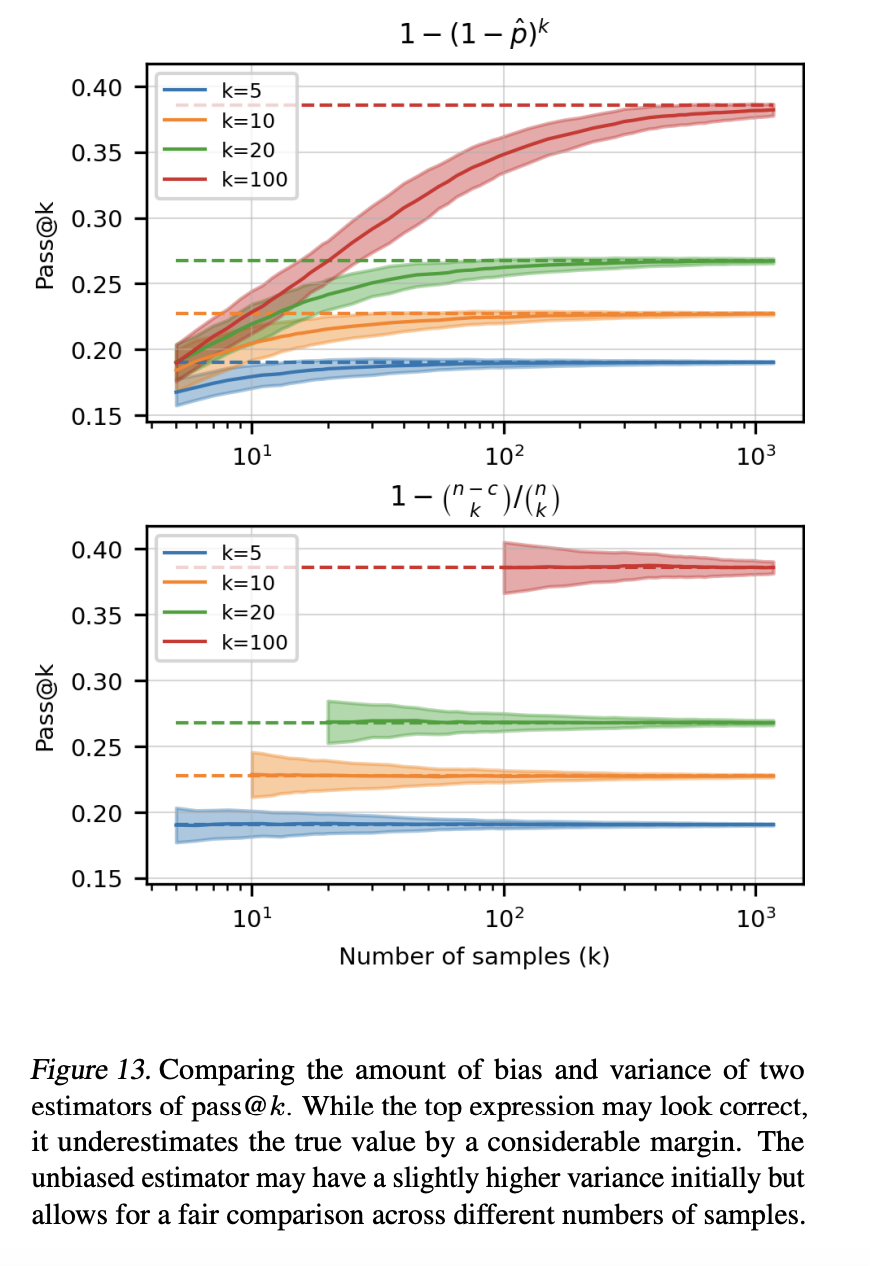
\[\text{pass@}k = 1 - (1 - \hat{p})^k\]

However, this is a biased estimator. The term $(1 - \hat{p})^k$ represents the probability that all $k$ samples fail, calculated as the product of $k$ independent failure probabilities. This multiplication only works when each sample is independent, meaning we’re drawing with replacement from an infinite population or putting samples back after each draw.

But in reality, when we select k samples from our n generated samples, we’re sampling without replacement. Once we pick a sample, we do not put it back. This means:

  • If our first sample is incorrect, we have one fewer incorrect sample in the pool
  • The probability of selecting another incorrect sample changes from $(n-c)/n$ to $(n-c-1)/(n-1)$ for $\text{pass@}1$.
  • The samples are no longer independent events

This mismatch between the formula’s assumption of independent draws with replacement and the reality dependent draws without replacement causes us to systematically underestimate the true $\text{pass@}k$.

OpenAI illustrated this issue in Chen et al, 2021.

OpenAI Codex

U-Statistics and the Unbiased Estimator

OpenAI’s solution uses U-statistic (the letter ‘U’ stand for unbiased, not the shape) to create an unbiased estimator. U-statistics are a class of statistics that provide minimum-variance unbiased estimators for parameters that can be expressed as expected values of symmetric functions.

Their estimator is:

\[\text{pass@}k = 1 - \frac{\binom{n-c}{k}}{\binom{n}{k}}\]

where:

  • $n$ is the total number of samples
  • $c$ is the number of correct samples
  • $k$ is the number of samples we’re considering

This formula calculates the probability that all $k$ selected samples are incorrect (from the $n-c$ incorrect samples), then subtracts from 1 to get the probability that at least one is correct.

Special Case: When $k=1$

When $k=1$, the unbiased estimator simplifies beautifully:

\[\text{pass@}1 = 1 - \frac{\binom{n-c}{1}}{\binom{n}{1}} = 1 - \frac{n-c}{n} = \frac{c}{n}\]

Number of correct samples divided by total number of sampels is exactly $\hat{p}$, our empirical success rate. This makes intuitive sense: when we only select one sample, there’s no difference between sampling with or without replacement. We’re just picking one sample from our pool. The probability of success is simply the proportion of successful samples, which validates that our unbiased estimator reduces to the correct simple case.

Why This Estimator is Better

  1. Unbiased: The expected value of this estimator equals the true $\text{pass@}k = 1 - (1 - p)^k$
  2. Accounts for finite sampling: It correctly handles sampling without replacement from a finite set
  3. Minimum variance: Among all unbiased estimators, U-statistic provide the minimum-variance estimate

Practical Example

Suppose you generate $n=10$ code samples and $c=3$ are correct:

  • Naive estimator: $\text{pass@}5 = 1 - (1 - 0.3)^5 = 1 - 0.7^5 = 0.83193$
  • Unbiased estimator: $\text{pass@}5 = 1 - \frac{\binom{7}{5}}{\binom{10}{5}} = 1 - \frac{21}{252} = 0.91667$

The unbiased estimator gives a significantly higher probability (91.7%) compared to the naive estimator (83.2%). This difference occurs because the naive estimator treats each draw as independent, while the unbiased estimator correctly accounts for the fact that we’re selecting 5 samples from a finite pool of 10 without replacement. The difference becomes more pronounced with smaller sample sizes or when k approaches n.

Applications in AI Systems

Understanding $\text{pass@k}$ helps us interpret benchmarks and design better AI systems.

Evaluation and Benchmarking

When models are evaluated on benchmarks like HumanEval or MBPP:

  • $\text{pass@}1 = 70\%$ means a single attempt has 70% chance of being correct
  • $\text{pass@}10 = 90\%$ means at least one of 10 attempts will likely be correct
  • This gap reveals the potential benefit of sampling multiple solutions

The metric extends beyond code to mathematical problem solving (AIME, GSM8K) and reasoning tasks, where verification is often programmatic.

Majority Voting Design Pattern

$\text{pass@k}$ insights can be applied as a design pattern in compound AI systems:

  • Self-Consistency: Generate k responses and use majority voting 
    def self_consistency(prompt, model, k=5):
  responses = [model.generate(prompt, temperature=0.7) for _ in range(k)]
  # Return most common answer or execute and verify for code/math
  return most_common(responses)

  • Best-of-N: Generate $N$ candidates, score them with a verifier, return the best

  • Temperature tuning: Higher temperature increases diversity (better $\text{pass@k}$ for $k>1$), while lower temperature improves $\text{pass@}1$

If $\text{pass@}10$ is significantly higher than $\text{pass@}1$, implementing multi-sampling could improve reliability though this trades off against latency and cost.

Conclusion

The $\text{pass@}k$ metric is a fundamental evaluation tool in LLM benchmarks, but its meaning is often misunderstood. Rather than simply counting how many attempts it takes to pass a test, $\text{pass@}k$ represents the probability that at least one of k independently sampled solutions is correct.

Key takeaways:

  • $\text{pass@}1$ is not about “passing on the first try” but rather the probability of a single sample being correct
  • Due to randomness in model outputs, we need estimators to calculate $\text{pass@}k$ from finite samples
  • The naive estimator is biased and underestimates the true $\text{pass@}k$
  • OpenAI’s unbiased estimator provides accurate estimates by properly accounting for sampling without replacement
  • The gap between pass@1 and pass@k reveals opportunities for improving reliability through multi-sampling

Understanding these technical definitions helps us better interpret model performance claims and benchmark results. When you see “$\text{pass@}1 = 92\%$” in the next model release, you’ll know it means the model has a 92% probability of generating a correct solution in a single attempt, calculated using an unbiased statistical estimator.

References

@misc{lee2025passk,
    author = {Lee, Hanchung},
    title = {Statistics for AI/ML, Part 4: pass@k with Unbiased Estimator},
    year = {2025},
    month = {09},
    howpublished = {\url{https://leehanchung.github.io/blogs/2025/09/08/pass-at-k/}},
    url = {https://leehanchung.github.io/blogs/2025/09/08/pass-at-k/}
}