Statistics for AI/ML, Part 1: Adding Confidence Interval to Your Aggregation Statistics
A major intersection between Artificial Intelligence and Machine Learning (AI/ML) and statistics is evaluation. Evaluation of AI/ML systems typically involves feeding $n$ inputs into the system to generate outputs $Y$. These results, depending on the task, can range from numeric values to classes or unstructured data such as text and images. Evaluation metrics might not always be statistical in nature—e.g., BERTScore or LLM-as-a-Judge for ordinal labels—but can be enhanced with statistical tools like confidence intervals. In this post, we’ll explore how to add a confidence interval to a classification task.
Bootstrap Resampling for Bootstrap Confidence Interval
A fundamental challenge in statistics is assessing the variability of an estimate derived from sample data. Bootstrap resampling is a statistical technique that estimates uncertainty when theoretical calculations are infeasible. Here’s how it works:
- Randomly sample $N$ observations from the dataset with replacement. Sampling with replacement means a data point can appear multiple times in a resampled dataset.
- Calculate the aggregation statistic (e.g., mean, median) for this resampled dataset.
- Repeat the process many times (1,000+ iterations).
- Calculate the mean and standard error of the aggregation statistic from these iterations for reference.
- Derive the desired confidence interval directly using percentile. This enables non-parametric measurements.
The elegance of bootstrapping is that it
- non-parametric: makes no assumption about the underlying data distribution.
- computational driven: flexible to work with any statistic
- provides a sense of how much a statistic might vary if data collection is done again
The mental model is simple: if the original sample is representative of the population, then resampling from it simulates drawing new samples from the population. The variation among bootstrap samples reflects the uncertainty of the estimate.
Note: Small datasets (size $n < 30$) might produce unstable or biased confidence intervals because the resamples lack diversity. This is a feature, not a bug.
Implementing Bootstrap Resampling
Let’s walk through an implementation of Bootstrap Confidence Interval. Imagine we have an AI agent acting as a binary classifier, producing outputs labeled as True or False for downstream tasks. Given 100 data samples with known labels:
- The agent correctly predicts 80 cases and incorrectly predicts 20.
- Accuracy is calculated as $80/100 = 80%$.
We aim to add a 95% confidence interval to this accuracy estimate. Recall that a 95% CI includes the middle 95% of the distribution:
[----|--------------------|----]
^ ^
2.5th 97.5th
|____________________|
95% of data
Here’s the implementation:
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(78) # humanity's last hope. iykyk
# Initialize Data
n_samples = 100
n_correct = 80
n_incorrect = 20
data = [1] * n_correct + [0] * n_incorrect
# Bootstramp Resampling parameters
n_iter = 10000
bootstrap_accuracies = []
# Bootstrapping
# 3. repeat the process many times
for _ in range(n_iter):
# 1. Resample with replacement
resample = np.random.choice(data, size=n_samples, replace=True)
# 2. Calculate the aggregation statistic.
accuracy = np.mean(resample)
bootstrap_accuracies.append(accuracy)
# 4. calculatemean and standard error
bootstrap_means = np.mean(bootstrap_accuracies)
bootstrap_stderr = np.std(bootstrap_accuracies)
# 5. Calculate desired confidence interval. Let's do 95%.
confidence_interval = np.percentile(bootstrap_accuracies, [2.5, 97.5])
# Print it out, plot it out.
print(f"Original mean: {np.mean(data):.2f}")
print(f"Bootstrap mean: {bootstrap_means}")
print(f"95% CI: ({confidence_interval[0]:.2f}, {confidence_interval[1]:.2f})")
plt.hist(bootstrap_accuracies, bins=30, density=True, alpha=0.7, label='Bootstrap accuracies')
plt.title('Distribution of Bootstrap Accuracies')
plt.xlabel('Accuracy')
plt.ylabel('Density')
plt.show()
Expected output:
Original mean: 0.80
Bootstrap mean: 0.8007050000000001
95% CI: (0.72, 0.88)
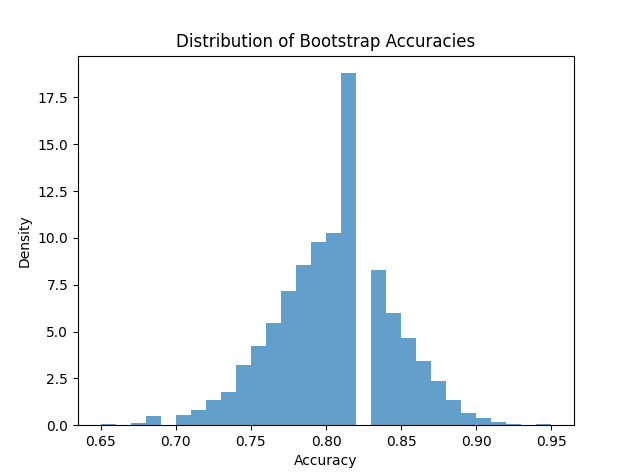
This means the estimated accuracy is 80% and we are 95% confident that the true accuracy of the AI agent lies between 72% to 88%.
Alternatives
Apart from Bootstrap Resampling, there are other methods to calculate confidence intervals. Here’s a comparison:
| Method | Description | Advantages vs Bootstrap | Disadvantages vs Bootstrap |
|---|---|---|---|
| Bootstrap Resampling | Randomly resamples the data with replacement to generate a distribution of the statistic. | - No strong assumption about data distribution. - Works for small or non-parametric datasets. - Applicable to any statistic (e.g., accuracy) |
- Sensitive to the quality of the data and resampling process. |
| Normal Approximation (z-interval) | Assumes the samplling distribution of the mean or proportion is normal, based on Central Limit Theorem (CLT), calculates CI using z-scores | - Simpler to calculate - Faster computation - Closed form solution |
- Requires large sample size - Assumes normal distribution - Less accurate for skewed data |
| Student’s t-interval | Similar to z-interval but uses t-distribution for small samples | - Better for small samples - Has theoretical foundation - Simple formula |
- Still assumes underlying normality - Only works for means - Less flexible for complex statistics |
| Wilson Score (for proportions) | Special method for binary outcomes using adjusted formula | - More accurate for proportions - Works well at extreme probabilities - Faster than bootstrap |
- Only works for proportions - More complex formula - Less intuitive |
| Jackknife Resampling | Leaves out one observation at a time | - Less computationally intensive - Good for bias estimation - More deterministic |
- Less accurate than bootstrap - Can’t handle non-smooth statistics well - Produces narrower intervals |
Bootstrap Resampling is best for general purpose use, especially when the data is non-parametric or the statistic is complex.
References
@article{
leehanchung,
author = {Lee, Hanchung},
title = {Statistics for AI/ML, Part 1: Adding Confidence Interval to Your Aggregation Statistics},
year = {2024},
month = {12},
howpublished = {\url{https://leehanchung.github.io}},
url = {https://leehanchung.github.io/blogs/2024/12/23/bootstrap-resampling/}
}