Reasoning Series, Part 4: Reasoning with Compound AI Systems and Post-Training
The previous two methods of implementing reasoning and inference-time scaling, prompt engineering and sampling, both share a critical drawback: there isn’t a well-defined way to verify the steps the model has taken or validate its outputs. This limitation significantly hinders the reasoning capabilities of large language models (LLMs). Imagine a $10%$ error rate at each step of the reasoning process. After just five steps, the error rate compounds to $1 - (1 - 0.1)^5 \approx 41\%$. To ensure reliability and robustness in reasoning, verification and validation are crucial. In this post, we explore how to achieve more reliable reasoning using compound AI systems and post-training LLMs.
Approach 3: Compound AI Systems
To incorporate verification and validation into the reasoning process, we can break a single LLM invocation with a long prompt into multiple LLM invocations with shorter prompts. This approach is called a compound AI system. These systems use multiple components connected in a reasoning path, rather than relying on a monolithic model inference as in previous methods.
Pros:
- Flexible design that can leverage existing engineering and systems techniques.
- Decouples the dependency between the underlying model and the overall system.
Cons:
- Increased complexity.
- Not all problems have clearly defined validation criteria.
- Higher latency.
- Reduced benefits from scaling compute across the system.
The use of validators in LLM reasoning can be understood through computational complexity theory. The class $P$ consists of decision problems solvable on a deterministic machine in polynomial time (i.e., quickly solvable problems). The class $NP$, meanwhile, consists of problems whose positive solutions are verifiable in polynomial time given the right information (i.e., quickly verifiable problems). P (quickly solvable) is a subset of NP (quickly verifiable). A common example is Sudoku: verifying a solution is easy, but generating one takes much longer.
In summary, verifying solutions is easier than finding them (similar to P ⊆ NP in computational complexity theory).
Translating this to LLMs, we can scale up reasoning or inference-time scaling if the verification cost is lower than the generation cost. This concept, termed the Generator-Verifier Gap, was named by OpenAI’s Noam Brown. For instance, if we have a quick golden validator, such as a code runtime, we can scale up our reasoning by searching or sampling to find the correct solution.
Now, let’s go through common reasoning design patterns for compound AI systems. And before that, lets establish some terminologies. In computer science and engineering, verification means to check the development results on if it satisfies the specification. Validation means that we checking the final product to see if it meets user requirements. In the discussions below, we might use them interchangeably.
Behavioral Pattern: Verification
The first reasoning design pattern is Verification. It involves verifying a step of a reasoning process or validating an LLM’s output, following a simple two-step process:
- LLM generates an answer.
- LLM verifies whether the answer is acceptable.
This pattern was explored in the early days by Cobbe et al., 2021, where the authors trained a 6B model in the GPT-3 family to verify the output of a 175B GPT-3 model in solving the GSM8k (Grade School Math) dataset. Similar methods have been used, such as self-critique (Saunders et al., 2022) for assisting human labeling of topic-based summarization tasks.
A common variation of this is Self-Verification (Weng et al., 2022), which involves:
- LLM generates candidate answers through sampling.
- LLM verifies these answers, computing a verification score.
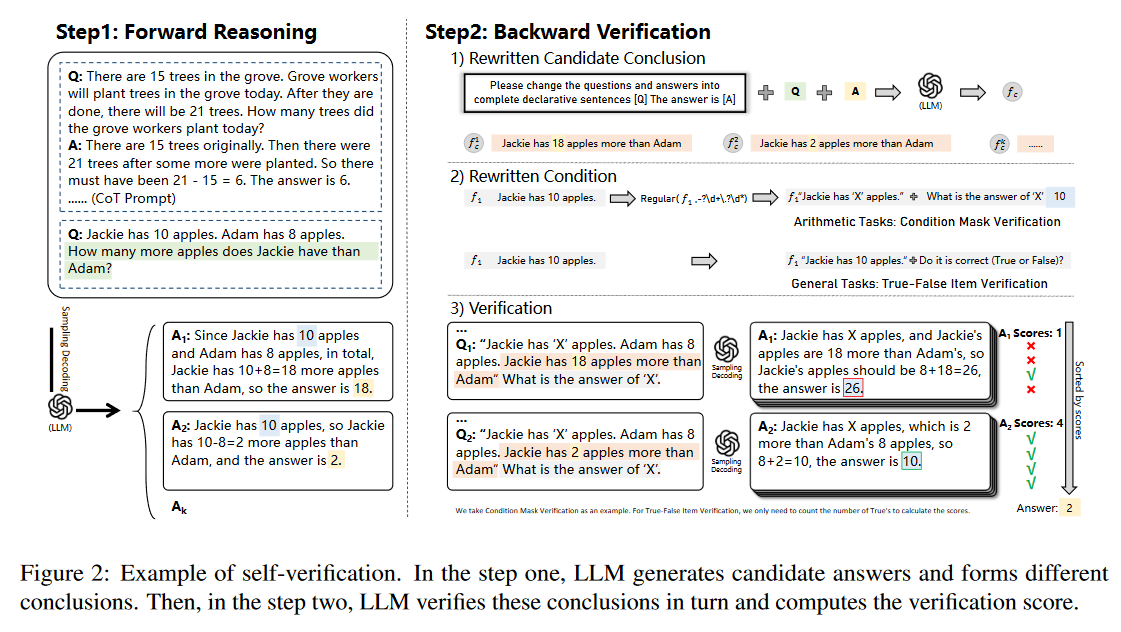
The idea of Self-Verification to sample several candidate answers and verify and score them, which we can distill down by first principles and remove the sampling from the equation and arrive at verification.
In tasks where clear judgment is difficult (e.g., summarization, speech writing), using LLM-as-a-Judge can work well for verification, though it may be insufficient for problems with well-defined solutions. In these cases, using external tools (e.g., code runtimes or math solvers) for verification is often more reliable—an approach called CRITIC (Gou et al., 2023) or ToRA (Gou et al, 2023).
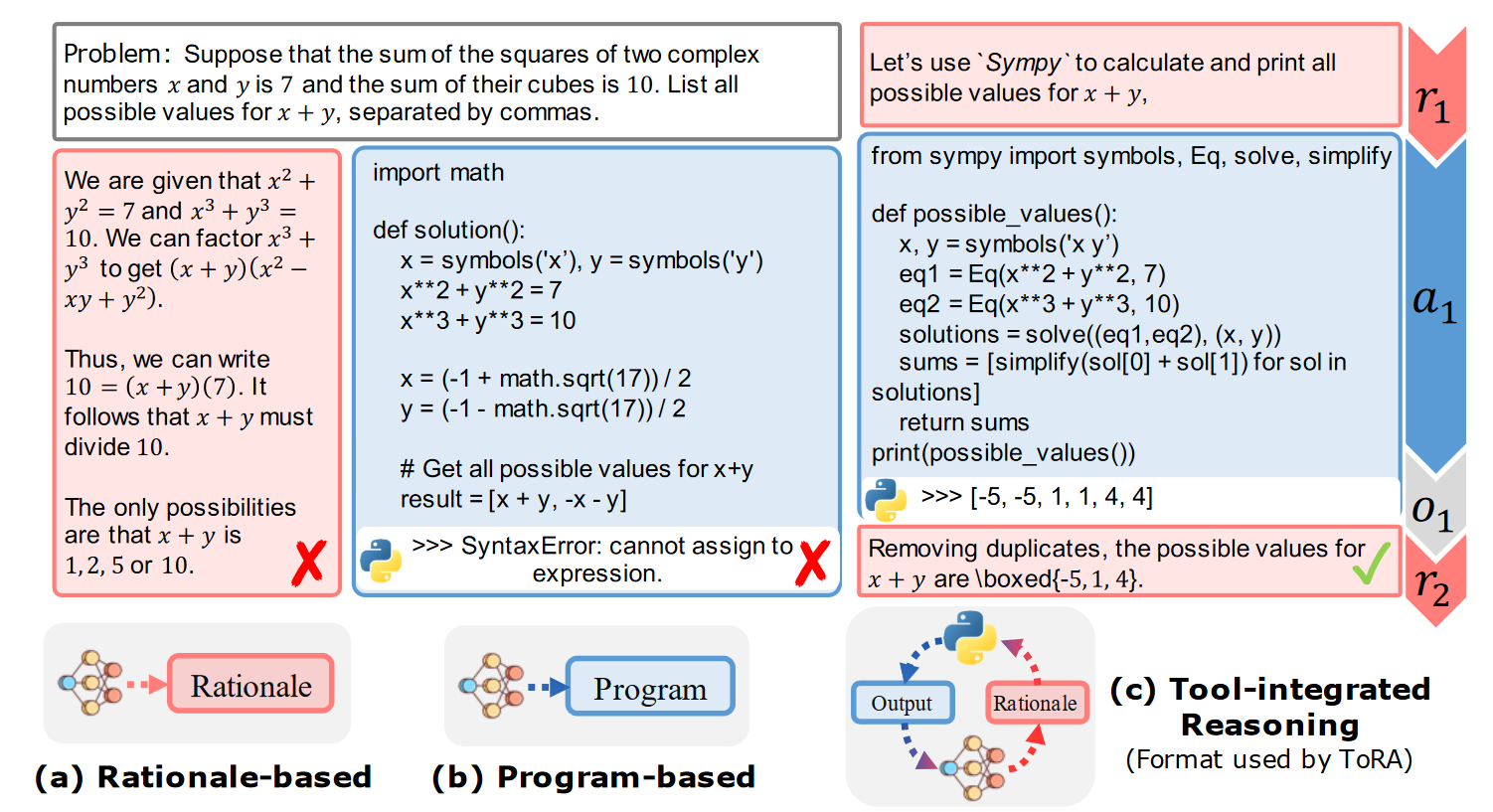
Note: Using the LLM itself for self-critique is a Rationale-based approach, related to our
Rationaleprompt engineering structural pattern.
Structural Pattern: majority voting
The first structural pattern is majority voting. This pattern samples from LLM(s) multiple times and selects the most frequent answer as the output. By sampling on multiple reasoning trajectories, this method provides higher-quality answers.
Self-Consistency (Wang et al., 2022) proposed sampling an LLM to generate several reasoning paths, then choosing the most consistent answer by majority vote.
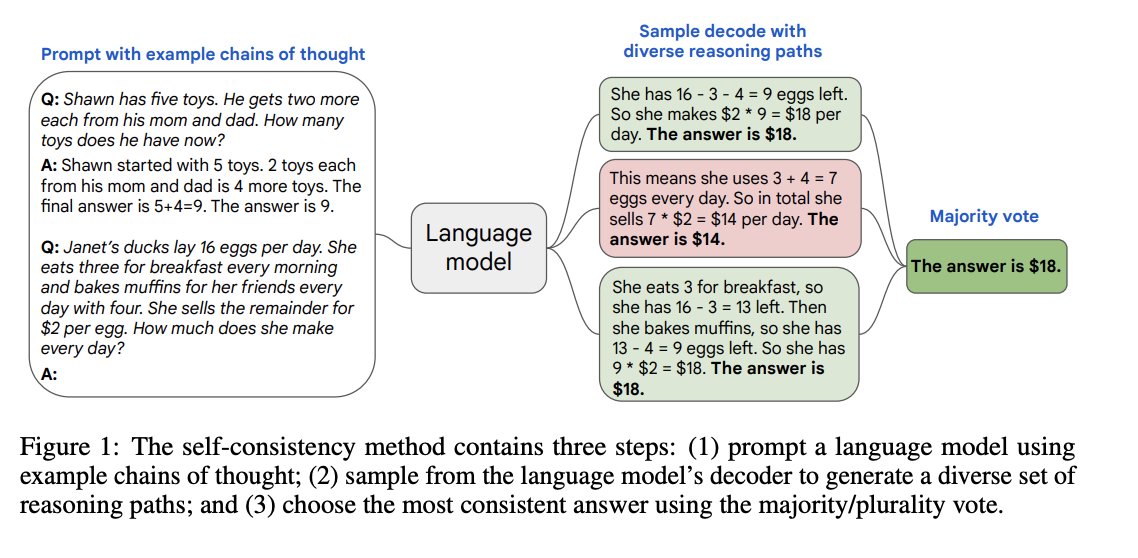
Extensions of this pattern, such as using “agents” (Li et al., 2024), majority voting at different abstraction levels.
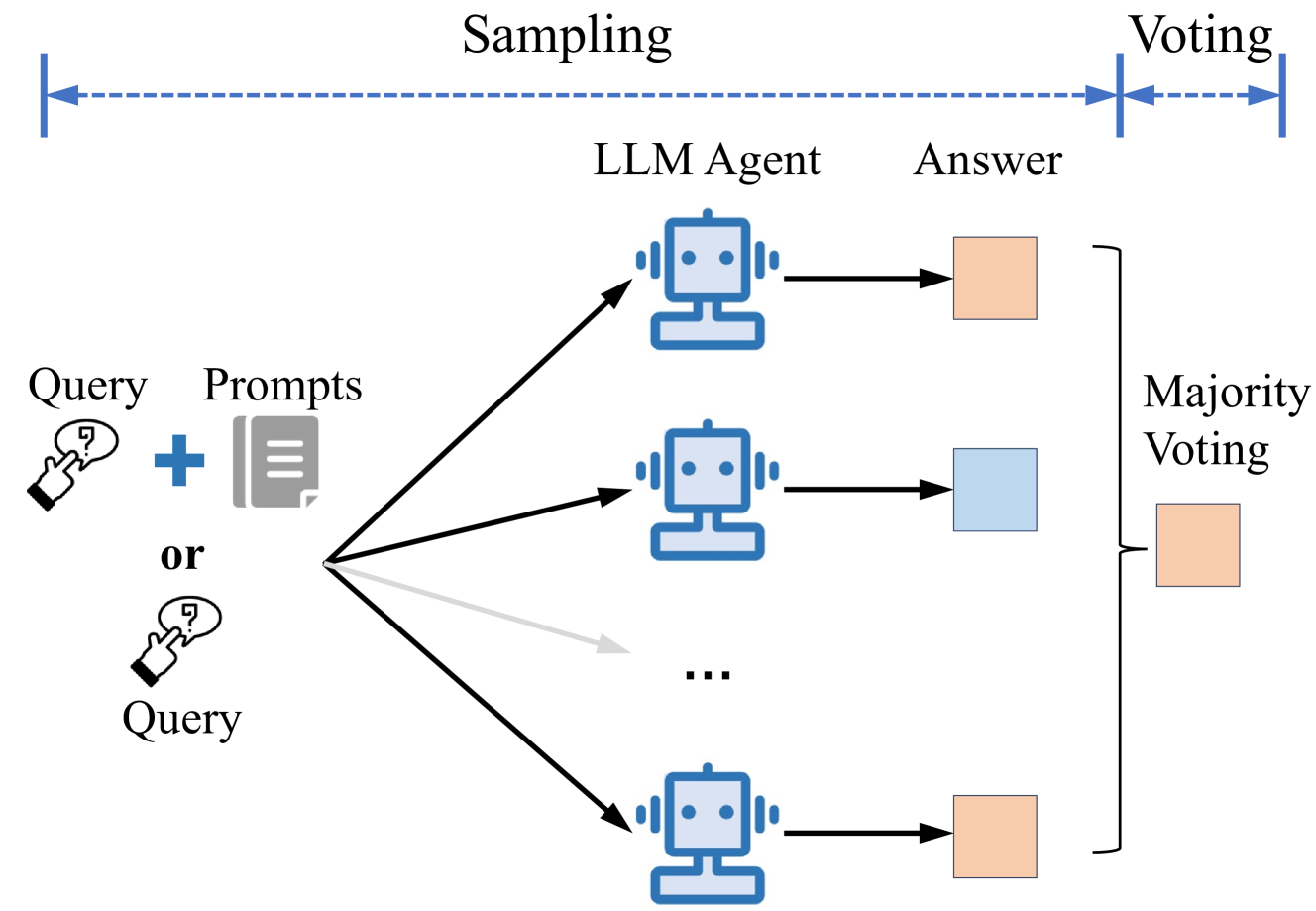
Variants include sampling with different prompts or LLMs, or using different voting thresholds (e.g., majority vote, 2/3 vote).
This pattern is often combined with Verification to add fresh knowledge by sampling from multiple LLMs or different strategies—though it can be costly if verification is expensive. Or, alternatively, we can apply this majority voting pattern for verification purposes. Note that this does increase the cost of reasoning tremendously and might tip the scale of generation vs verification costs.
Structural Pattern: Reasoning Tools
Now we covered the basic behavioral patterns to build an reasoning compound AI systems, we will now discuss on how we can stitch together basic patterns into structured systems. In common LLM agent literature, one of the component of LLM agents is tool use, which means calling external APIs for extra information or capabilities to make up the deficiencies of the LLM agent. Now, taking a step back from this, we define
Reasoning Tools refer to using the LLM itself as an internal tool to compose a more robust reasoning agent.
Prominent examples of Reasoning Tools include ReAct (Yao et al., 2022), Self-Reflection (Renze et al., 2024), Self-Refine (Madaan et al., 2023), and Reflexion (Shinn et al., 2023).
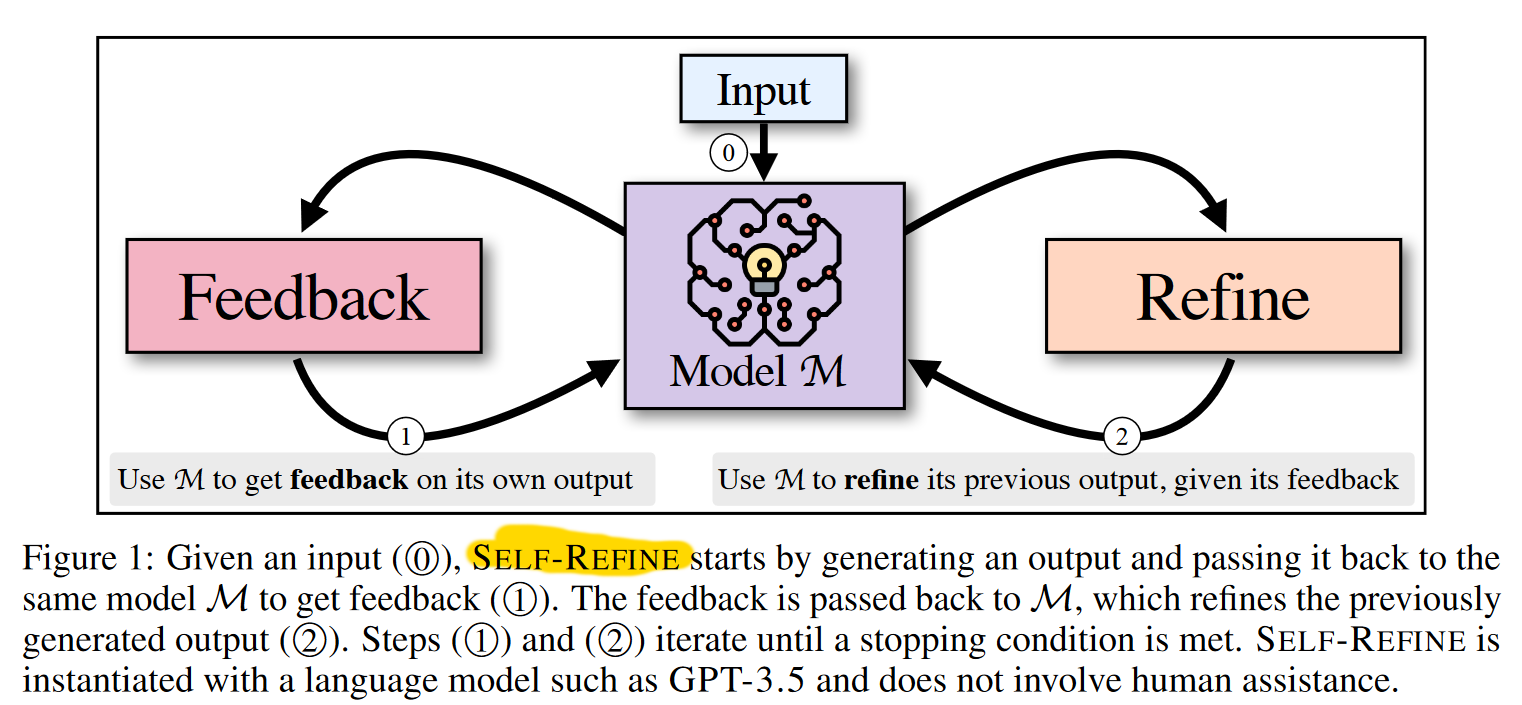
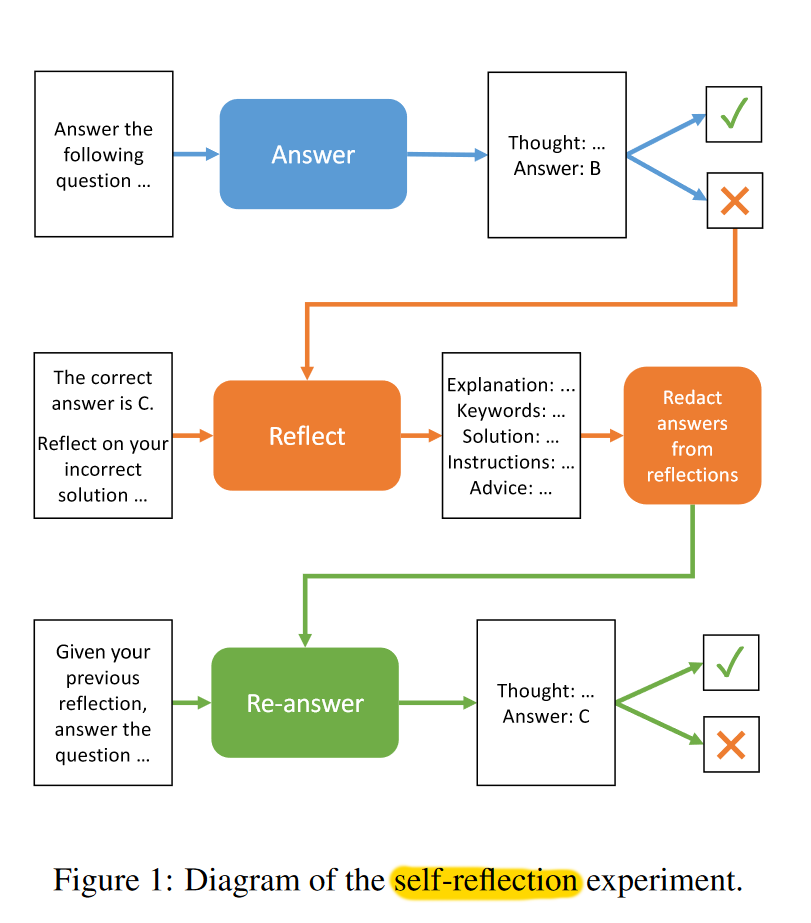
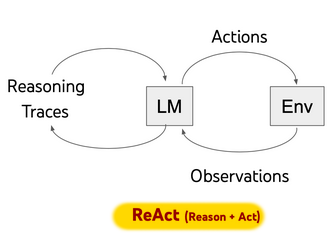
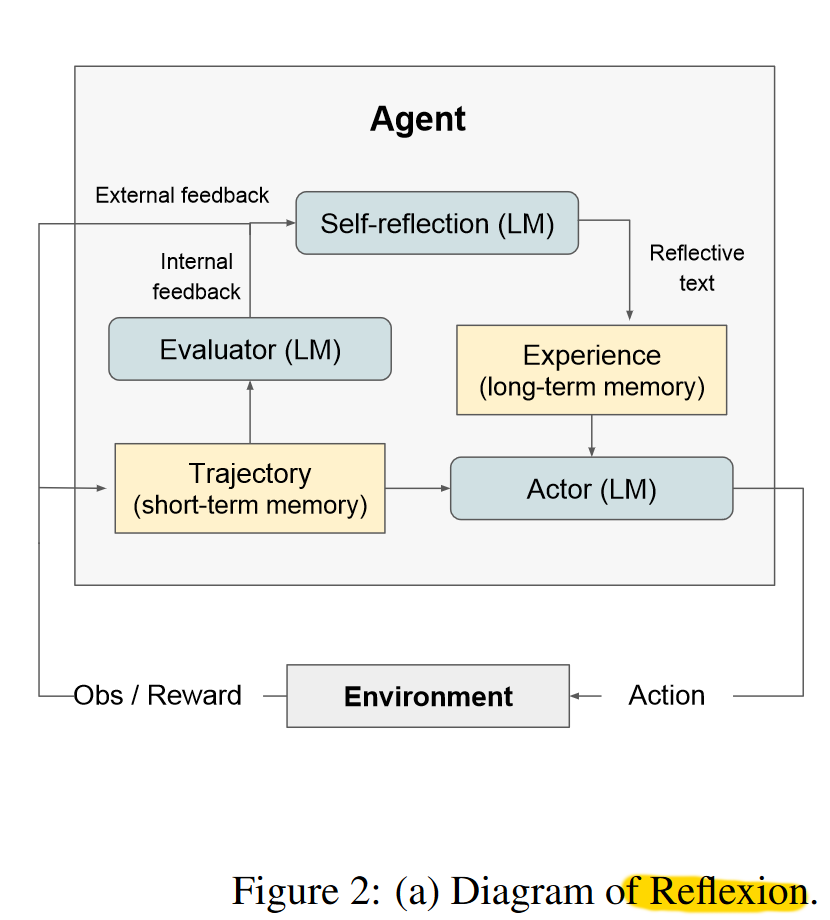
These systems may appear different, but they can all be modeled as a sequence of agent actions where the actions are determined by the agent. We can model them by Markov decision process in reinforcement learning. Reinforcement learning (RL) is an interdisciplinary area of machine learning and optimal control concerned with how an intelligent agent should take action in a dynamic environment in order to maximize a reward signal. it involves a set of environment and agent states, $S$ , a set of actions (action space) available for the agent $A$ , and the immediate reward $R_t$ after transition from $s$ to $s’$ under action $a$.
With the RL framework in mind, we can collapse all of the given actions shown on the above diagrams into a set of reasoning tools. These include reason, act, reflect, and refine. In addition, there’s evaluate and feedback for action, but we can fold these into the verification pattern mentioned above. Since majority voting pattern above also produces an output, we can and should add it to our action space as one of the options. With this organization of all these exploratory framework papers, we can then collapse them all together into an RL diagram below.
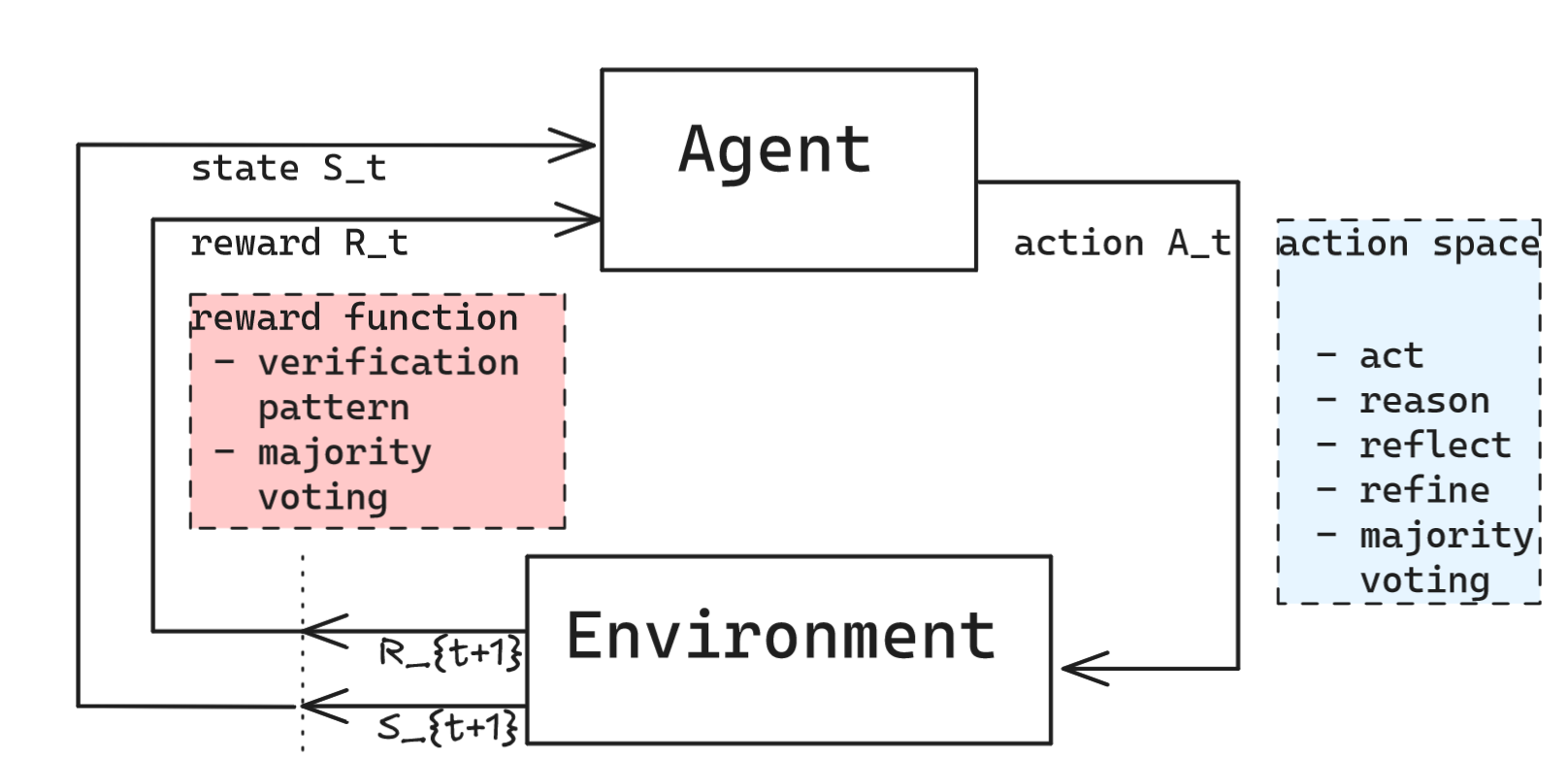
Note that the verification pattern is not considered a reasoning tool specifically because its used to determine rewards of the action space, not used as an action. This parallels the reward models in reinforcement learning from human feedbacks (RLHF) in LLM post training process.
NOTE: reward modeling is a lot easier for tasks with deterministic and crisp rewards, e.g., coding and math, vs tasks with ambigious and messy rewards, e.g., content generation, summarization, etc. We will solve International Math Olympiad before solving summarization.
With this consolidation, then all of the above reasoning patterns and proposals, from ReAct to Reflexion, can be modeled as a sequence of agentic actions, where the actions are determined by the agent. Or conversely, these proposed reasoning patterns are unrolling of sequential reasoning tools use by agents, where the actions are pre-defined by the developers.
NOTE: the unrolling of reasoning tools can be considered a reasoning trajectory. This is one of the key concept that leads to reasoning for post training in the later discussions.
Structural Pattern: Search
The Verification pattern also enables AI search algorithms like breadth-first, depth-first, or Monte Carlo Tree Search (MCTS) to iteratively search through the potential reasoning trajectories.
This was popularized by Tree of Thought (Yao et al., 2023) and its variations, such as Graph of Thought (Besta et al., 2023). These methods explore reasoning paths using verification to determine which paths to pursue or prune, similar to classic search algorithms from AI literature. The only difference is that we are using LLMs or external validators to evaluate the state at each node in the search tree. We recommend reviewing Artificial Intelligence: A Modern Approach to understand different ways to use search to solve problems instead of chasing LLM flavored papers on Arxiv.

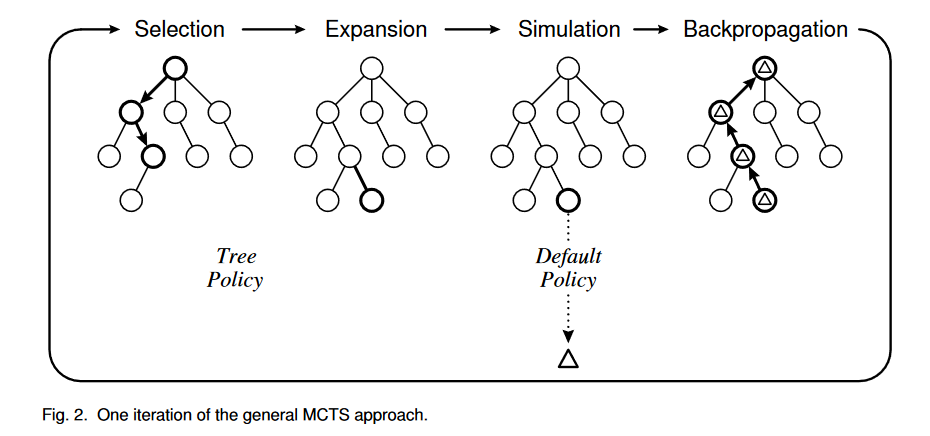
In addition to the classic search algorithms, one of the prominent search algorithm is Monte Carlo Tree Search (MCTS). In essence, it applies Monte Carlo method to the search problem by iteratively goes through selection -> expansion -> simulation -> back propagation process to estimate values of seach search nodes.
MCTS was studied extensively for playing Go games for more than a decade before AlphaGo. Combined with reinforcement learning, it created success for super-human abilities. For better understanding of MCTS, we recommend A Survey of Monte Carlo Tree Search Methods (Browne et al, 2012).
NOTE: There are two places we can implement search for LLMs; at the systems level with an external verifier in compound AI systems, and at the decoding sampling level. Verification at the decoding sampling level is limited due to latency and signals available.
Add tool use and memory, we can compose all current compound AI systems for reasoning with these design patterns, with potentially some variations on the same theme. These robust ways of building reasoning into AI systems are, however, only scalable at best sub linearly with scale in compute. Specifically, with more compute, these reasoning design patterns remains largely static and at most has better latency.
In the next method, we will discuss how to potentially scale reasoning with compute.
Method 4: Post-Training for Reasoning (Speculation)
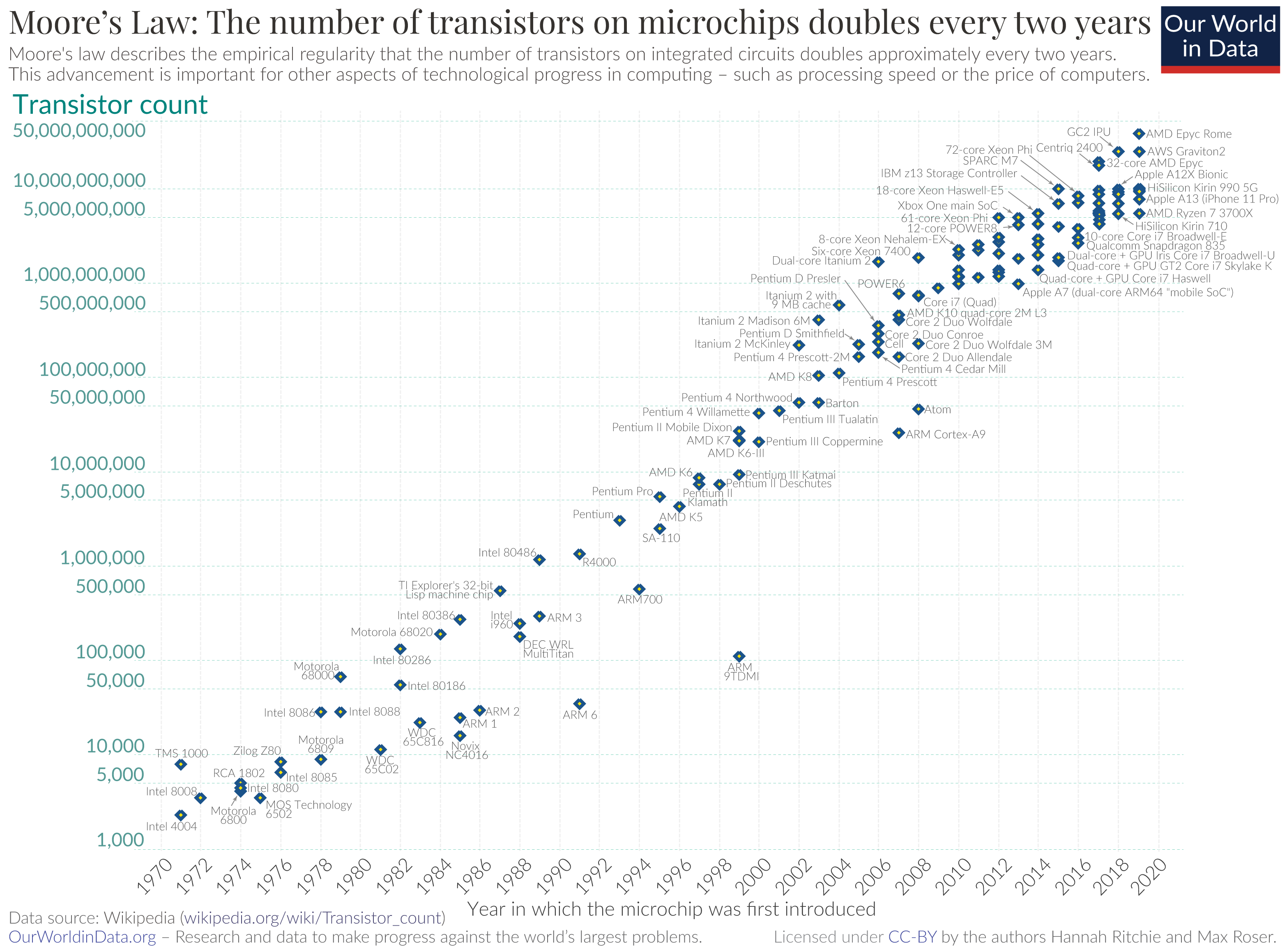
The biggest contributor to technological progress over the past several decades is Moore’s Law. Moore’s Law loosely predicts that the number of transistors on integrated circuits will double every two years with minimal rise in cost. Moore’s Law has powered technological progress, from miniaturization to the Internet. Any technology that couples itself with Moore’s Law will, at the very least, be able to scale along its exponential curve. For example, the growth in Internet traffic is enabled by semiconductors scaling up with Moore’s Law. The same applies to the growth of storage size and throughput. In this sense, all technologies that benefit from Moore’s Law can be considered as scaling compute.
LLMs are no different. There was a split in direction after the introduction of Transformers (Vaswani et al, 2017). One direction focused on encoder-only models like BERT (Devlin et al, 2018), while the other focused on decoder-only models like GPT (Radford et al, 2018). The BERT family of models dominated research until ChatGPT. The key innovation of the GPT model is its autoregressive nature, which combined scalability with both compute and data, eventually surpassing the BERT family of models.
All previously mentioned methods of implementing reasoning attempt to squeeze more reasoning capabilities out of existing models and thus do not scale with compute. To make reasoning scale with compute, there are now approaches that do so during the post-training phase. The key concept is the Linear Representation Hypothesis (Elhage et al, 2022).
“No matter what we want to do, we linearize it into a long sequence and put it into a transformer. And we make the transformer big enough and we see what it can do.” - Chris Manning, COLM 2024 Keynote
This is still an early research area, and it assumes that this hypothesis will work for reasoning traces. We will try our best to cover the current known research. Some of the information covered is speculative, as we do not know exactly how OpenAI’s o1 model was trained.
Pros:
- Flexible design that can apply existing engineering and systems techniques.
- Takes advantage of Moore’s Law, which scales exponentially.
- Decouples the dependency between the underlying model and the overall system.
- Models can be utilized effectively.
Cons:
- Requires building process reward models and objective reward models for post-training.
- Requires Reinforcement Learning from Human Feedback (RLHF) Ouyang et al, 2022 post-training on reasoning trajectories, which might cause unintended behaviors.
- Significant data requirements involving generating synthetic reasoning trajectories using active learning techniques.
- Hard to control reasoning trajectories using prompts or validators.
- Expensive to use over APIs.
As a quick synopsis, imagine a system built using the design patterns covered in Method 3, where we flatten the agentic action steps into linear sequences as reasoning trajectories. To evaluate the outputs of every step of the process and the final outputs, we can employ the verifier design pattern components as reward models for the reasoning trajectories. With these, we can then use the reasoning trajectories data and reward models to post-train LLMs with RLHF. This forms the basis of scaling reasoning during inference time.
As an example, here’s a way of flattening reasoning trajectories (Zhang et al, 2023) of the search design pattern (depth-first search and breadth-first search) into sequences.
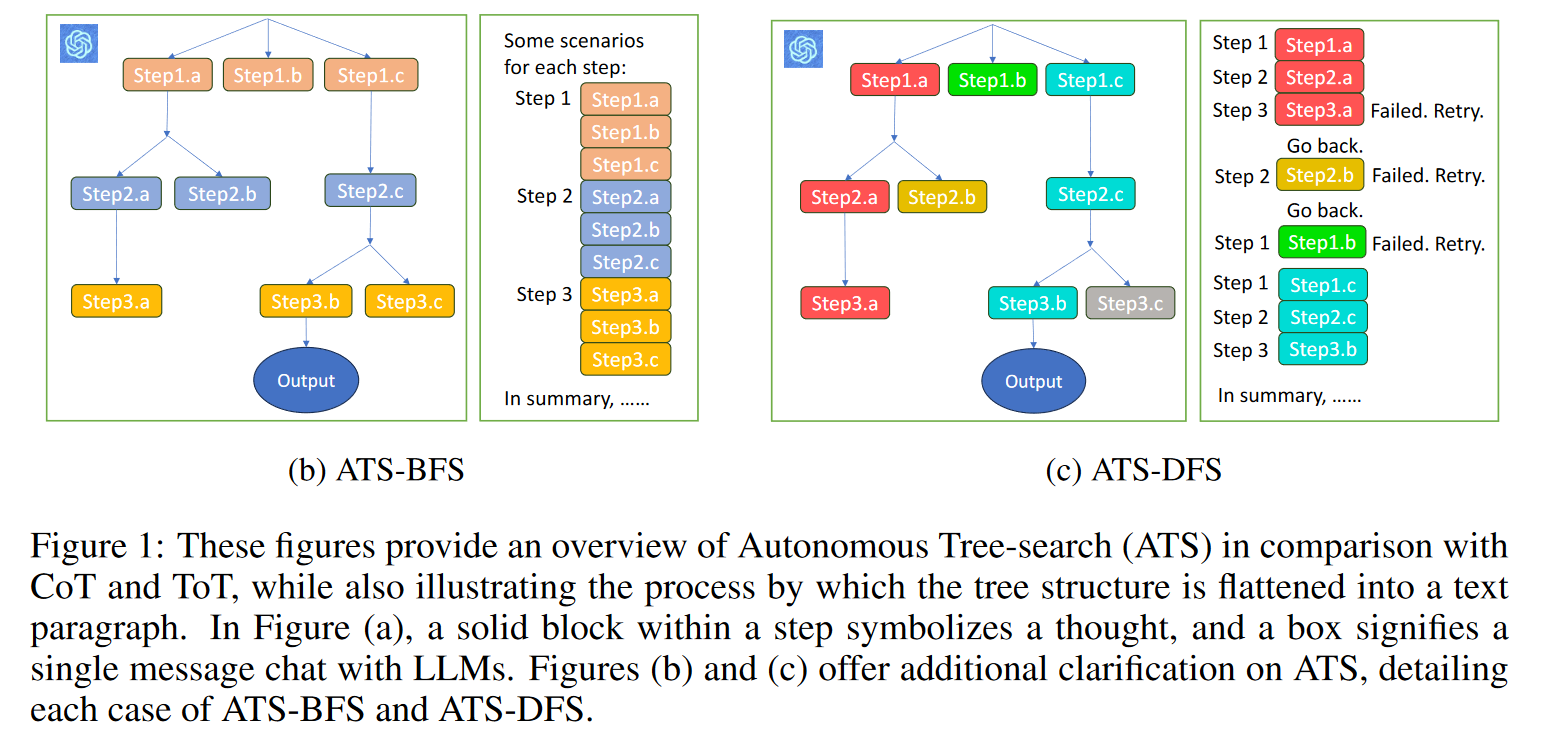
Before we dive into the details of post-training LLMs for reasoning, let’s review the current post-training paradigm.
Review: Post-Training Reinforcement Learning from Human Feedback (RLHF)
Currently, LLM training is divided into two phases: pre-training and post-training. In the pre-training stage, we primarily focus on feeding the model as much data as possible to build out its knowledge, intuition, and understanding of the world. This process primarily concerns handling large amounts of data and the engineering involved in scaling up infrastructure and ensuring the robustness of the training process.
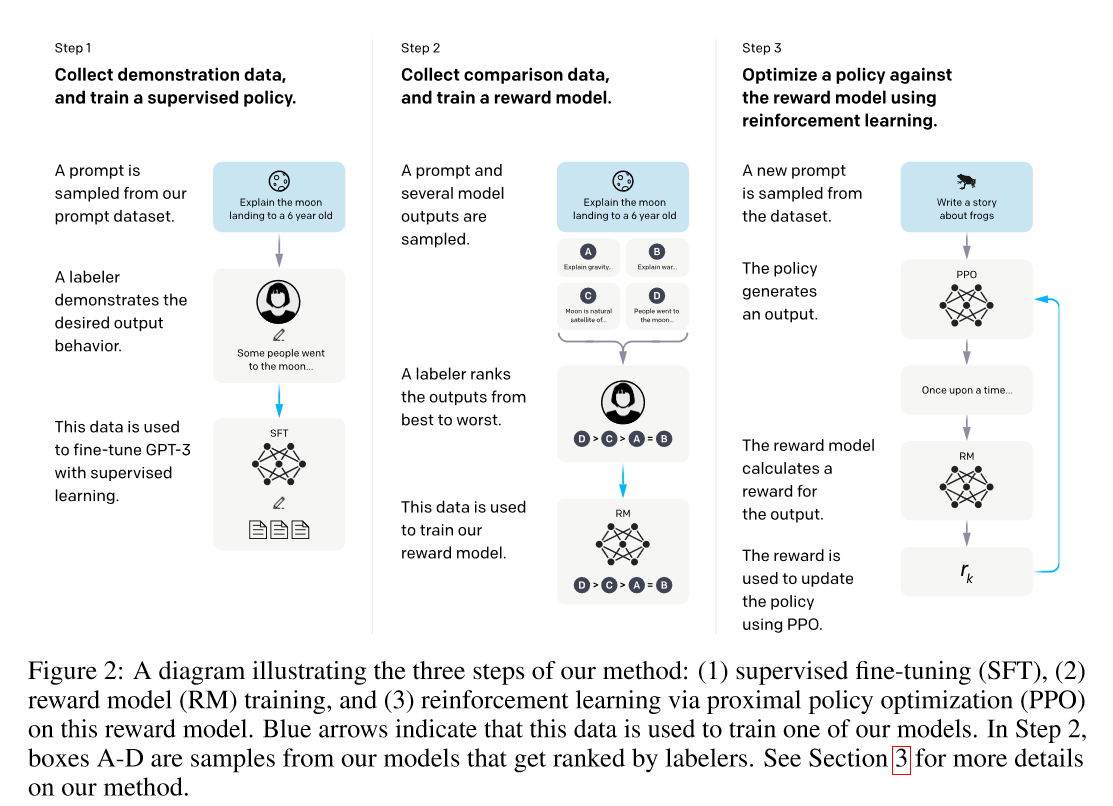
In the post-training phase, we take the pre-trained model with its knowledge and world understanding, and train it to follow human instructions. The post-training process is well documented in (Ouyang et al, 2022). It starts with supervised fine-tuning (SFT) to train the model with labeled question-answer pairs (step 1). Then it trains the model using reinforcement learning from human feedback (RLHF) with the proximal policy optimization algorithm (PPO) (Schulman et al, 2017) (step 3) with a reward model trained in step 2. Note that we frame the RLHF problem by treating the LLM as policy $\pi$ in step 3, aiming to optimize the policy $\pi$ to generate outputs with the highest rewards.
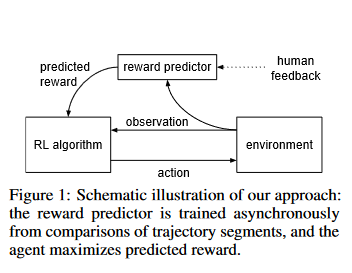
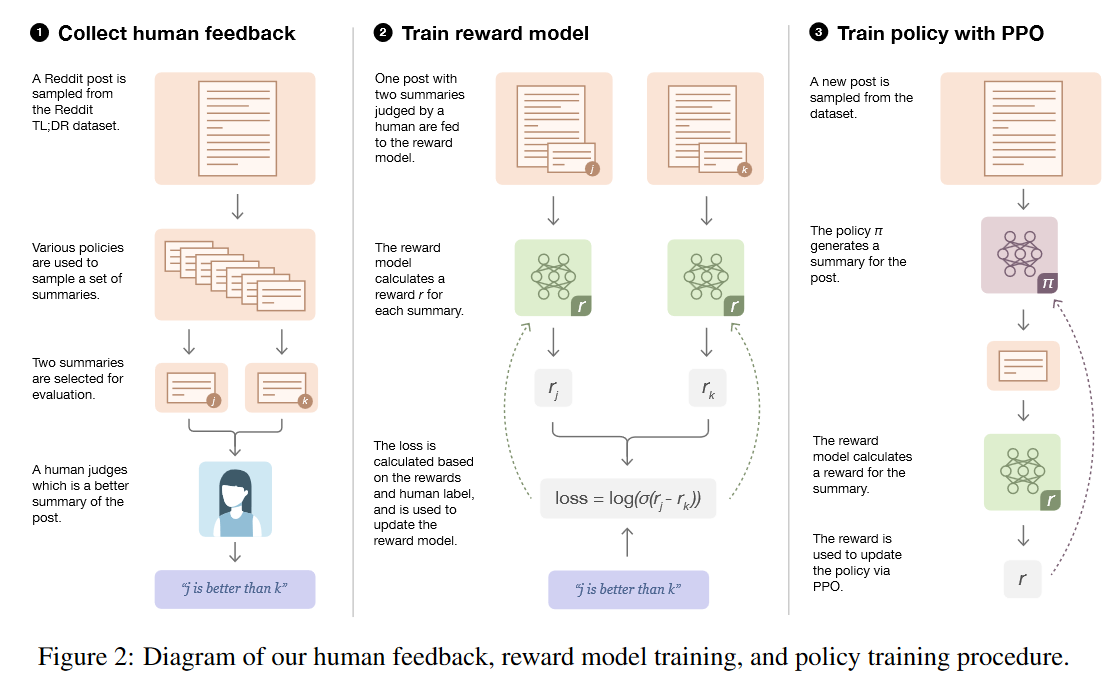
The early RLHF process was developed by (Christiano et al, 2017) and later applied to one of the most challenging NLP tasks, summarization (Stiennon et al, 2020). The process centers around a reward model to assign values, allowing for backpropagation and learning using PPO. It has significant data requirements. In addition, the reward models are typically built by supervised fine-tuning (SFT) a smaller LLM, in this case, 6B GPT-3 models as the reward model. The role of the reward model is to provide a scalar value to score the output. In other words, the reward model serves the same function as the verifier in compound AI systems.
Post-Training for Reasoning
Researchers have shown that the reasoning abilities of LLMs improve with chain-of-thought (CoT) prompting (Kojima, 2022). However, there’s a mismatch between what we think CoT reasoning is and what the model is actually doing. CoT was more about imitating reasoning patterns seen in pretraining data , e.g., math and coding solutions, or in-context learning few-shot examples (CoT@k). These reasoning patterns are examples and rationales written out by humans ex post, not the actual thought process as humans have when they solve the problems.
This is post-trained with Reinforcement Learning from Human Feedback (RLHF) using objective reward models (ORMs) that evaluated the final outputs only, much like scoring a math problem solely based on whether the final answer is correct. This does not provide the nuances of reasoning.
One of the potential solution to fix this deficiency is with the new post-training for reasoning paradigm. Instead of aligning the model to output the highest reward results, we can utilize process-supervised reward models (PRMs) (Uesato et al, 2022; Lightman et al, 2023) to align the model’s reasoning trajectory alongside the intermediate steps, rewarding progress throughout the reasoing trajectory. With this, we hope that model would have a richer and more genuine reasoning path instead of some ex post explanations of reasoning.
We postulate that OpenAI teaches its reasoning model (o1) to improve its reasoning capabilities by using both PRMs to guide reasoning trajectories and ORMs to ensure that the desired reasoning results are achieved. There are significant technical challenges in doing this, including scaling up RLHF training with both PRMs and ORMs, and generating sufficiently large and high-quality datasets from both human-labeled data (RLHF) and AI-labeled data (RLAIF).
One mystery that remains unresolved is how OpenAI seems to be able to control the number of reasoning tokens used, as indicated in their report.
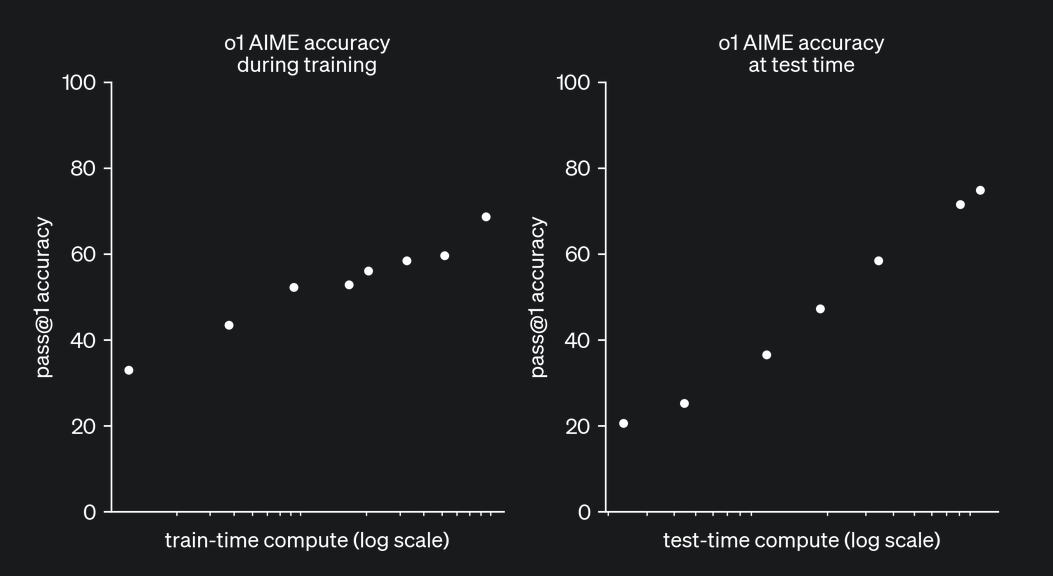
We believe this opens an exciting path for model self-alignment, similar to AlphaZero self-play. Both the model and the reward model share the same pre-trained base, allowing the model to learn from itself and align automatically. Like AlphaZero, which improved by playing against itself, an LLM could refine its reasoning by generating, verifying, and adjusting its own outputs using internal feedback.
This self-supervised process lets the model critique and improve its reasoning with minimal external data, making alignment more scalable and less reliant on costly human supervision. The feedback loop helps the model become more robust and accurate over time.
This approach could also lead to models that adapt better to new problems. By learning from successes and failures, the model builds a deeper understanding of complex tasks, leading to skills that go beyond explicit training. The key advantage is the potential for exponential growth in reasoning ability as the model iteratively refines its decision-making and alignment.
References
- Zaharia, M., Khattab, O., Chen, L., Davis, J. Q., Miller, H., Potts, C., Zou, J., Carbin, M., Frankle, J., Rao, N., & Ghodsi, A. (2024). The shift from models to compound AI systems. BAIR Blog. Retrieved from https://bair.berkeley.edu/blog/2024/02/18/compound-ai-systems/
- Cobbe, K., Kosaraju, V., Bavarian, M., Chen, M., Jun, H., Kaiser, L., Plappert, M., Tworek, J., Hilton, J., Nakano, R., Hesse, C., & Schulman, J. (2021). Training Verifiers to Solve Math Word Problems. arXiv. https://arxiv.org/abs/2110.14168
- Saunders, W., Yeh, C., Wu, J., Bills, S., Ouyang, L., Ward, J., & Leike, J. (2022). Self-critiquing models for assisting human evaluators. arXiv. https://arxiv.org/abs/2206.05802v1
- Weng, Y., Zhu, M., He, S., Liu, K., & Zhao, J. (2022). Large Language Models are reasoners with Self-Verification. arXiv. https://arxiv.org/abs/2212.09561v1
- Gou, Z., Shao, Z., Gong, Y., Shen, Y., Yang, Y., Duan, N., & Chen, W. (2023). CRITIC: Large Language Models Can Self-Correct with Tool-Interactive Critiquing. arXiv. https://arxiv.org/abs/2305.11738v1
- Gou, Z., Shao, Z., Gong, Y., Shen, Y., Yang, Y., Huang, M., Duan, N., & Chen, W. (2023). ToRA: A Tool-Integrated Reasoning Agent for Mathematical Problem Solving. arXiv. https://arxiv.org/abs/2309.17452v1
- Wang, X., Wei, J., Schuurmans, D., Le, Q., Chi, E., & Zhou, D. (2022). Self-Consistency Improves Chain of Thought Reasoning in Language Models. arXiv. https://arxiv.org/abs/2203.11171v1
- Li, J., Zhang, Q., Yu, Y., Fu, Q., & Ye, D. (2024). More Agents Is All You Need. arXiv. https://arxiv.org/abs/2402.05120v1
- Yao, S., Zhao, J., Yu, D., Du, N., Shafran, I., Narasimhan, K., & Cao, Y. (2022). ReAct: Synergizing Reasoning and Acting in Language Models. arXiv. https://arxiv.org/abs/2210.03629v1
- Renze, M., & Guven, E. (2024). Self-Reflection in LLM Agents: Effects on Problem-Solving Performance. arXiv. https://arxiv.org/abs/2405.06682v1
- Madaan, A., Tandon, N., Gupta, P., Hallinan, S., Gao, L., Wiegreffe, S., Alon, U., Dziri, N., Prabhumoye, S., Yang, Y., Welleck, S., Majumder, B. P., Gupta, S., Yazdanbakhsh, A., & Clark, P. (2023). Self-Refine: Iterative Refinement with Self-Feedback. arXiv. https://arxiv.org/abs/2303.17651v1
- Shinn, N., Cassano, F., Gopinath, A., Narasimhan, K., & Yao, S. (2023). Reflexion: Language Agents with Verbal Reinforcement Learning. In A. Oh, T. Naumann, A. Globerson, K. Saenko, M. Hardt, & S. Levine (Eds.), Advances in Neural Information Processing Systems (Vol. 36, pp. 8634–8652). Curran Associates, Inc. https://proceedings.neurips.cc/paper_files/paper/2023/file/1b44b878bb782e6954cd888628510e90-Paper-Conference.pdf
- Yao, S., Yu, D., Zhao, J., Shafran, I., Griffiths, T. L., Cao, Y., & Narasimhan, K. (2023). Tree of Thoughts: Deliberate Problem Solving with Large Language Models. arXiv. https://arxiv.org/abs/2305.10601v1
- Besta, M., Blach, N., Kubicek, A., Gerstenberger, R., Gianinazzi, L., Gajda, J., Lehmann, T., Podstawski, M., Niewiadomski, H., Nyczyk, P., & Hoefler, T. (2023). Graph of Thoughts: Solving Elaborate Problems with Large Language Models. arXiv. https://arxiv.org/abs/2308.09687v1
- Russell, S., & Norvig, P. (2020). Artificial Intelligence: A Modern Approach (4th ed.). Pearson.
- Browne, C., Powley, E., Whitehouse, D., Lucas, S., Cowling, P. I., Rohlfshagen, P., Tavener, S., Perez, D., Samothrakis, S., & Colton, S. (2012). A Survey of Monte Carlo Tree Search Methods. IEEE Transactions on Computational Intelligence and AI in Games, 4(1), 1-43. https://doi.org/10.1109/TCIAIG.2012.2186810
- Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., & Polosukhin, I. (2017). Attention Is All You Need. arXiv. https://arxiv.org/abs/1706.03762v1
- Devlin, J., Chang, M.-W., Lee, K., & Toutanova, K. (2018). BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. arXiv. https://arxiv.org/abs/1810.04805v1
- Radford, A., Narasimhan, K., Salimans, T., & Sutskever, I. (2018). Improving Language Understanding by Generative Pre-Training. OpenAI. https://cdn.openai.com/research-covers/language-unsupervised/language_understanding_paper.pdf
- Elhage, N., Hume, T., Olsson, C., Schiefer, N., Henighan, T., Kravec, S., Hatfield-Dodds, Z., Lasenby, R., Drain, D., Chen, C., Grosse, R., McCandlish, S., Kaplan, J., Amodei, D., Wattenberg, M., & Olah, C. (2022). Toy Models of Superposition. https://transformer-circuits.pub/2022/toy_model/index.html
- Manning, C. (2024). Meaning and Intelligence in Language Models: From Philosophy to Agents in a World [COLM 2024 Keynote] [Video]. YouTube. https://www.youtube.com/watch?v=c3N2H3Z5S3I&t=2016s
- Ouyang, L., Wu, J., Jiang, X., Almeida, D., Wainwright, C. L., Mishkin, P., Zhang, C., Agarwal, S., Slama, K., Ray, A., Schulman, J., Hilton, J., Kelton, F., Miller, L., Simens, M., Askell, A., Welinder, P., Christiano, P., Leike, J., & Lowe, R. (2022). Training language models to follow instructions with human feedback. arXiv. https://arxiv.org/abs/2203.02155
- Zhang, Z., Ye, Z., Shen, Y., & Gan, C. (2023). Autonomous Tree-search Ability of Large Language Models. arXiv. https://arxiv.org/abs/2310.10686
- Schulman, J., Wolski, F., Dhariwal, P., Radford, A., & Klimov, O. (2017). Proximal Policy Optimization Algorithms. arXiv. https://arxiv.org/abs/1707.06347v1
- Stiennon, N., Ouyang, L., Wu, J., Ziegler, D. M., Lowe, R., Voss, C., Radford, A., Amodei, D., & Christiano, P. (2020). Learning to summarize from human feedback. arXiv. https://arxiv.org/abs/2009.01325v1
- [Kojima, T., Gu, S. S., Reid, M., Matsuo, Y., & Iwasawa, Y. (2022). Large Language Models are Zero-Shot Reasoners. arXiv. ]https://arxiv.org/abs/2205.11916v1](https://arxiv.org/abs/2205.11916v1)
- Uesato, J., Kushman, N., Kumar, R., Song, F., Siegel, N., Wang, L., Creswell, A., Irving, G., & Higgins, I. (2022). Solving math word problems with process- and outcome-based feedback. arXiv. https://arxiv.org/abs/2211.14275
- Lightman, H., Kosaraju, V., Burda, Y., Edwards, H., Baker, B., Lee, T., Leike, J., Schulman, J., Sutskever, I., & Cobbe, K. (2023). Let’s Verify Step by Step. arXiv. https://arxiv.org/abs/2305.20050
@article{
leehanchung,
author = {Lee, Hanchung},
title = {Reasoning Series, Part 4: Reasoning with Compound AI Systems and Post-Training},
year = {2024},
month = {11},
howpublished = {\url{https://leehanchung.github.io}},
url = {https://leehanchung.github.io/blogs/2024/11/22/reasoning-agents-post-training/}
}